Пусть R и S два векторных пространства размерности n и m соответственно над числовым полем K, и пусть A линейный оператор отображающий R в S . Выясним, как меняется матрица оператора A при изменении базисов в пространствах R в S.
Выберем произвольные базисы в пространствах R в S и обозначим через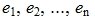 
и
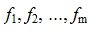соответственно. Тогда (см. в линейные операторы) векторному равенству
| y=Ax. | (1) |
соответствует матричное равенство
| y=Ax. | (2) |
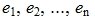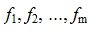где х и у векторы x и y, представленные в виде координатных столбцов в базисах и соответственно.
Выберем теперь в пространствах R и S другие базисы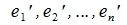 
и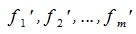
. В новых базисах векторному равенству (1) будет соответствовать матричное равенство
| y'=A'x'. | (3) |
Обозначим через Q и P невырожденные квадратные матрицы порядков n и m соответственно, которые осуществляют преобразование координат в пространствах R и S при переходе от старых базисов к новым (см. линейное пространство). Тогда связь между векторами в старых и новых базисах можно представить следующими равенствами:
| x'=Qx, y'=Py. | (4) |
Тогда, учитывая (3) и (4), имеем
| y'=Py=PAx=PAQ-1x'. | (5) |
Обозначив T=Q−1, и учитывая (3) и (5) получим:
| A'=PAT. | (6) |
Определение 1. Две прямоугольные матрицы A и B одинаковых размеров называются эквивалентными, если существуют две квадратные невырожденные матрицы P и T такие, что выполнено равенство
| B=PAT. | (7) |
Отметим, что если A -матрица порядка m×n, то P и T квадратные матрицы порядков m и n, соответственно.
Из (6) следует, что две матрицы, соответствующие одному и тому же линейному оператору A при различном выборе базисов в пространствах R и S эквивалентны между собой. Верно и обратное утверждение. Если матрица A соответствует оператору A, а матрица B эквивалентна матрице A, то она соответствует этому же линейному оператору A при других базисах в R и S.
Выясним, при каких условиях две матрицы эквивалентны.
Теорема. Для того, чтобы две матрицы одинаковых размеров были эквивалентны между собой, необходимо и достаточно, чтобы они имели один и тот же ранг.
Доказательство. Необходимость. Так как умножение матрицы на квадратную невырожденную матрицу не может изменить ранг матрицы, то из (7) имеем:
| rang B=rang A. |
Достаточность. Пусть задан линейный оператор A, отображающий пространство R в S и пусть этому оператору отвечает матрица A размера m×n в базисах 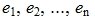в R и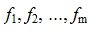 в S, соответственно. Обозначим через r число линейно независимых векторов из числа Ae1, Ae2,..., Aen. Пусть линейно независимы первые r векторы Ae1, Ae2,..., Aer. Тогда остальные n-r векторы выражаются линейно через эти векторы:
|
(8) |
Зададим новый базис в пространстве R:
 |
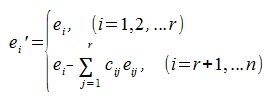Тогда учитывая (8), имеем:
  |
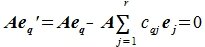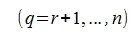(9) |
Далее выберем векторы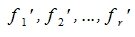 
в качестве векторов базиса в S:
| fj'=Aej', j=1,2,...,r | (10) |
Дополним эти векторы некоторыми векторами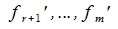 
до базиса в S.
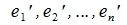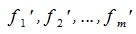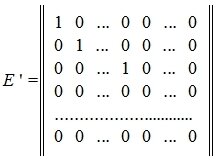
Тогда матрица оператора A в новых базисах , согласно (9) и (10) будет иметь следующий вид:
 |
(11) |
где в матрице E ' -на главной диагонали стоят r единиц, а остальные элементы равны нулю.
Так как матрицы A и E ' соответствуют одному и тому же оператору A, то они эквивалентны между собой. Выше мы показали, что эквивалентные матрицы имеют один и тот же ранг, следовательно ранг исходной матрицы A равен r.
Из вышеуказанного следует, что произвольная m×n матрица ранга r эквивалентна матрице E ' - порядка m×n. Но E ' - однозначно определяется заданием размерности m×n матрицы и его ранга r. Следовательно все прямоугольные матрицы порядка m×n и ранга r эквивалентны одной и той же матрице E ' и, следовательно, эквивалентны между собой.■